 Visualization of the biDMD algorithm.
Visualization of the biDMD algorithm.
Abstract
Data-driven methods for establishing quantum optimal control (QOC) using time-dependent control pulses tailored to specific quantum dynamical systems and desired control objectives are critical for many emerging quantum technologies. We develop a data-driven regression procedure, bilinear dynamic mode decomposition (biDMD), that leverages time-series measurements to establish quantum system identification for QOC. The biDMD optimization framework is a physics-informed regression that makes use of the known underlying Hamiltonian structure. Further, the biDMD can be modified to model both fast and slow sampling of control signals, the latter by way of stroboscopic sampling strategies. The biDMD method provides a flexible, interpretable, and adaptive regression framework for real-time, online implementation in quantum systems. Further, the method has strong theoretical connections to Koopman theory, which approximates nonlinear dynamics with linear operators. In comparison with many machine learning paradigms minimal data is needed to construct a biDMD model, and the model is easily updated as new data is collected. We demonstrate the efficacy and performance of the approach on a number of representative quantum systems, showing that it also matches experimental results.
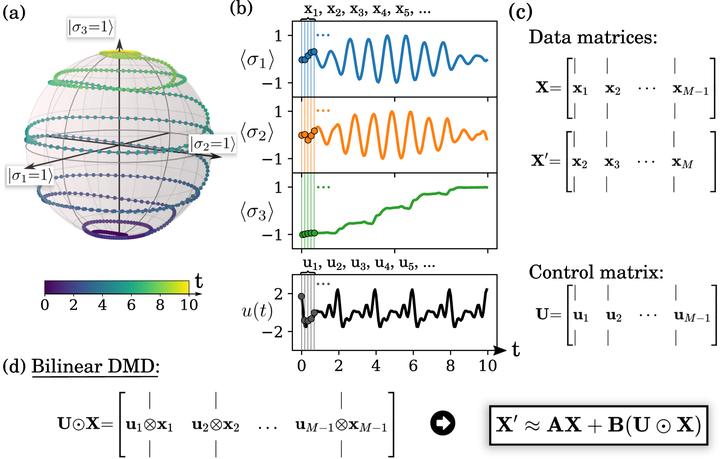
Caption for the figure: The trajectory of a qubit driven by a linearly-polarized semi-classical drive $\textrm{u}(t)$ (Hamiltonian: $H(t) = \pi \sigma_z + \textrm{u}(t) \sigma_x$) is shown on the Bloch sphere in (a). The corresponding Pauli-spin measurements are shown in (b). Measurements $\mathbf{x}_j$, $j=1,2,\dots$, are taken at discrete time steps and assembled into offset snapshot matrices $\mathbf{X}$ and $\mathbf{X}'$ in (c). The bilinear Dynamic Mode Decomposition (d) is a regression-based algorithm that uses the assembled data matrices and control input from sufficiently-resolved data to learn the intrinsic dynamics, $\mathbf{A}$ and the control, $\mathbf{B}$, for the bilinear dynamics.